Binary Tree Data Structure
Overview
This document covers the fundamental concepts of binary trees, including their structure, implementation, traversal methods, and common operations. We’ll explore how binary trees work, their properties, and practical applications in programming.
Why We Need Binary Trees?
1. Efficient Data Organization
Binary trees provide a natural way to organize hierarchical data with logarithmic time complexity for many operations.
Comparison of Data Structures:
| Operation | Array | Linked List | Binary Tree (BST) |
|-----------|-------|-------------|-------------------|
| Search | O(n) | O(n) | O(log n) |
| Insert | O(n) | O(n) | O(log n) |
| Delete | O(n) | O(n) | O(log n) |
| Traversal | O(n) | O(n) | O(n) |
Advantages:
- Faster search than linear structures
- Maintains sorted order automatically
- Efficient for large datasets
2. Natural Hierarchical Representation
Many real-world problems have inherent hierarchical structure that binary trees model perfectly.
Examples of Hierarchical Data:
File System:
📁 Root
├── 📁 Documents
│ ├── 📄 report.pdf
│ └── 📁 Projects
│ ├── 📄 project1.txt
│ └── 📄 project2.txt
└── 📁 Pictures
├── 📄 photo1.jpg
└── 📄 photo2.jpg
Organization Chart:
👤 CEO
├── 👤 Manager A
│ ├── 👤 Employee 1
│ └── 👤 Employee 2
└── 👤 Manager B
├── 👤 Employee 3
└── 👤 Employee 4
Decision Tree:
🤔 Should I go outside?
├── 🌧️ Is it raining? → No
│ └── 🚶 Go for a walk
└── 🌧️ Is it raining? → Yes
└── 🏠 Stay inside
3. Mathematical Expression Evaluation
Binary trees naturally represent mathematical expressions, enabling efficient evaluation and manipulation.
Expression: (3 + 4) * 2
Tree Representation:
*
/ \
+ 2
/ \
3 4
Benefits:
- Easy to evaluate: traverse and compute
- Simple to modify: change operators/operands
- Natural precedence handling
- Enables expression optimization
4. Database and File System Indexing
Binary search trees are fundamental to database indexing and file system organization.
Database Index Example:
User Table with BST Index on "age":
25
/ \
18 32
/ \ \
15 20 40
Search Process:
- Looking for age = 20
- Start at root (25)
- 20 < 25, go left to 18
- 20 > 18, go right to 20
- Found in 3 steps instead of scanning entire table
Performance Benefits:
- O(log n) search instead of O(n)
- Efficient range queries
- Automatic sorting
5. Memory Management
Binary trees help organize memory allocation and deallocation efficiently.
Memory Allocation Tree:
1024KB
/ \
512KB 512KB
/ \ / \
256KB 256KB 256KB 256KB
Benefits:
- Quick allocation of appropriate size
- Efficient merging of free blocks
- Minimizes memory fragmentation
- Fast deallocation and coalescing
6. Compiler Design
Abstract Syntax Trees (ASTs) are binary trees that represent program structure.
Code: x = a + b * c
AST Representation:
=
/ \
x +
/ \
a *
/ \
b c
Compiler Benefits:
- Natural precedence representation
- Easy code generation
- Simple optimization passes
- Clear program structure
7. Game Development and AI
Binary trees are essential for game trees, decision trees, and AI algorithms.
Game Tree (Tic-Tac-Toe):
X
/ | \
O O O
/|\ /|\ /|\
X X X X X X X
AI Applications:
- Minimax algorithm for game AI
- Decision trees for NPC behavior
- Pathfinding algorithms
- State space exploration
8. Network Routing
Binary trees help organize network routing tables and IP address lookups.
IP Address Routing Tree:
192.168
/ \
192.168.1 192.168.2
/ \ / \
.10 .20 .10 .20
Routing Benefits:
- Fast IP address lookup
- Efficient subnet management
- Quick routing table updates
- Hierarchical network organization
9. Priority Queues and Heaps
Binary heaps (specialized binary trees) provide efficient priority queue operations.
Max Heap Example:
100
/ \
80 60
/ \ /
50 70 40
Heap Operations:
- Insert: O(log n)
- Extract Max: O(log n)
- Build Heap: O(n)
- Priority queue management
10. Balanced Search Trees
Advanced binary trees (AVL, Red-Black) guarantee balanced structure for consistent performance.
AVL Tree Example:
30
/ \
20 40
/ \ \
10 25 50
Balancing Benefits:
- Guaranteed O(log n) operations
- Self-balancing after insertions/deletions
- Consistent performance regardless of input order
- Prevents degenerate cases
Real-World Impact
Performance Comparison
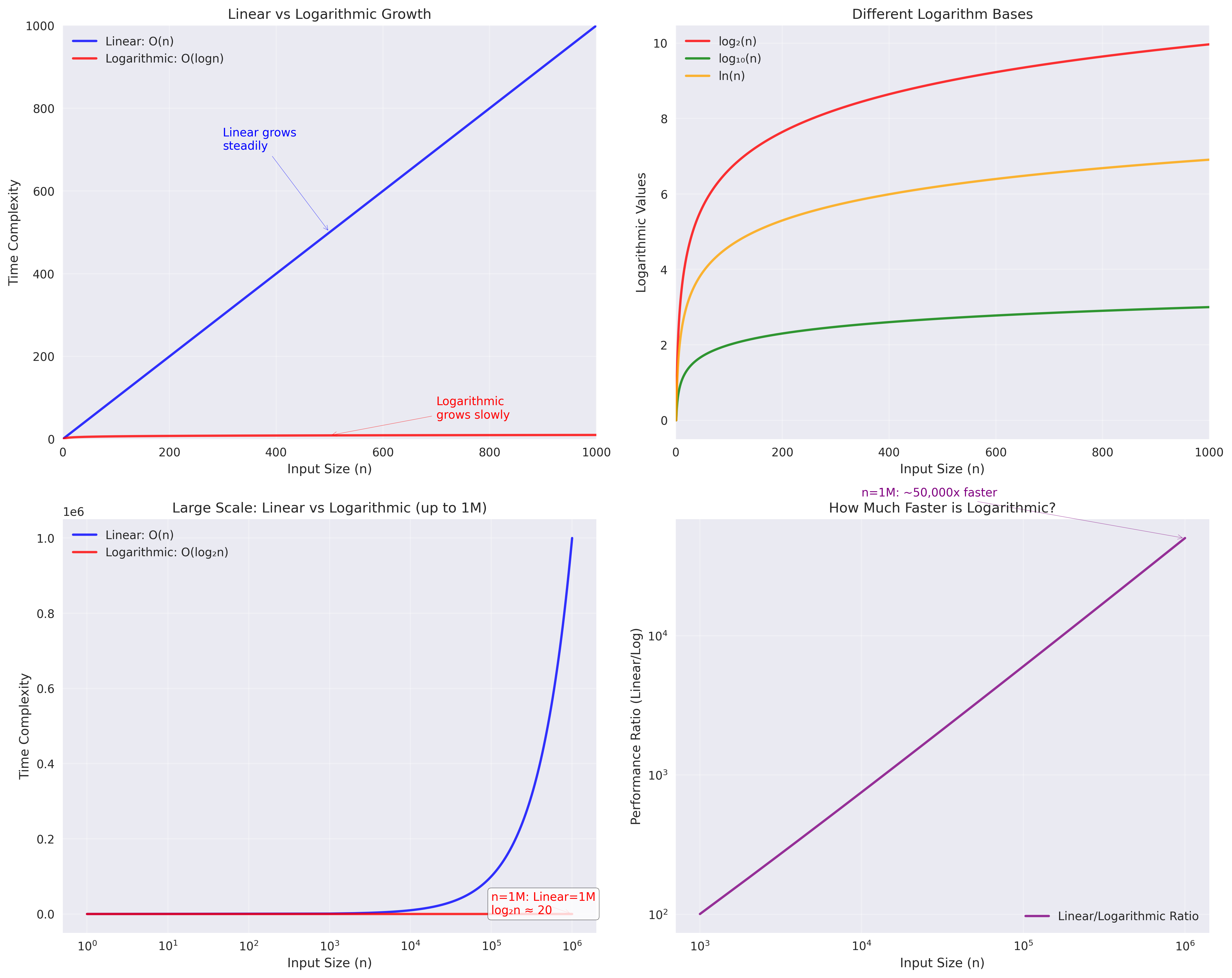
Figure: Time complexity comparison between linear O(n) and logarithmic O(log n) algorithms. The logarithmic growth (red line) shows dramatically better performance for large datasets.
Dataset Size: 1,000,000 elements
Linear Search (Array/Linked List):
- Average comparisons: 500,000
- Time: ~500ms
Binary Search Tree:
- Average comparisons: 20
- Time: ~0.02ms
Improvement: 25,000x faster!
Memory Efficiency
Storage Comparison:
- Array: Contiguous memory, potential waste
- Linked List: Extra pointers, fragmentation
- Binary Tree: Flexible allocation, efficient use
Memory Usage:
- Array: Fixed size, may waste space
- Binary Tree: Grows/shrinks as needed
- Better for dynamic data
Scalability
Growth Analysis:
Elements: 1K → 1M → 1B
Linear Structures:
- Search time: 1ms → 1s → 16min
Binary Trees:
- Search time: 0.01ms → 0.02ms → 0.03ms
Scalability: Binary trees scale logarithmically!
Detailed Mathematical Explanation
Why Linear Structures Grow Linearly?
Linear Search (Array/Linked List):
- Time Complexity: O(n)
- Need to check each element until target is found
- Average need to check n/2 elements
Mathematical Calculation:
1K elements: check 500 elements ≈ 1ms
1M elements: check 500,000 elements ≈ 1s
1B elements: check 500,000,000 elements ≈ 16min
Growth Pattern: Time ∝ Number of Elements
Why Binary Trees Grow Logarithmically?
Binary Search Tree:
- Time Complexity: O(log₂n)
- Each comparison eliminates half the elements
- Tree height = log₂(n)
Mathematical Calculation:
log₂(1K) = log₂(1000) ≈ 10 levels
log₂(1M) = log₂(1,000,000) ≈ 20 levels
log₂(1B) = log₂(1,000,000,000) ≈ 30 levels
Search Process Visualization:
1K elements: check at most 10 nodes
1M elements: check at most 20 nodes
1B elements: check at most 30 nodes
Growth Pattern: Time ∝ log₂(Number of Elements)
Search Process Comparison
Linear Search Process:
Find element 7 in array [1,2,3,4,5,6,7,8,9,10]:
Step 1: Check 1 → not found
Step 2: Check 2 → not found
Step 3: Check 3 → not found
Step 4: Check 4 → not found
Step 5: Check 5 → not found
Step 6: Check 6 → not found
Step 7: Check 7 → found!
Need to check 7 elements
Binary Tree Search Process:
Find element 7 in balanced binary tree:
5
/ \
3 8
/ \ / \
1 4 6 9
Step 1: Check root node 5 → 7 > 5, go to right subtree
Step 2: Check node 8 → 7 < 8, go to left subtree
Step 3: Check node 6 → 7 > 6, go to right subtree
Step 4: Found 7!
Only need to check 4 nodes
Why Logarithmic Growth is So Important?
As shown in the complexity comparison chart above, logarithmic growth provides dramatic performance advantages:
Data Size Growth Comparison:
Elements Linear Search Binary Tree Search Performance Gain
1K 1ms 0.01ms 100x
1M 1s 0.02ms 50,000x
1B 16min 0.03ms 32,000,000x
Key Insight:
- Linear structures: 1000x data increase = 1000x time increase
- Binary trees: 1000x data increase = ~1x time increase
Summary of Benefits
- Efficiency: O(log n) operations for search, insert, delete
- Hierarchy: Natural representation of hierarchical data
- Flexibility: Easy to modify and restructure
- Scalability: Performance doesn’t degrade with size
- Versatility: Applicable to diverse problem domains
- Memory: Efficient memory usage and allocation
- Balance: Can maintain balanced structure automatically
- Traversal: Multiple ways to visit all elements
- Optimization: Enables various algorithmic optimizations
- Foundation: Basis for more advanced data structures
Binary trees are not just a data structure—they are a fundamental tool that enables efficient solutions to countless real-world problems, from simple data organization to complex system design.
What is a Binary Tree?
Basic Concept
A binary tree is a hierarchical data structure where each node has at most two children, typically referred to as the left child and right child. Each node contains data and references to its children.
Key Properties
- Hierarchical Structure: Each node can have at most two children
- Single Root: One node serves as the starting point
- Unique Path: Each node has exactly one path from the root
- No Cycles: No node can reference back to an ancestor
Mathematical Representation
Tree Structure:
Root
/ \
Left Right
/ \ / \
L1 L2 R1 R2
Node Properties:
- Each node has at most 2 children
- Left child < Parent (in BST)
- Right child > Parent (in BST)
- Leaf nodes have no children
Generic Binary Tree Implementation
Generic Node Structure
class TreeNode<T extends Comparable<T>> {
T data; // Generic data stored in the node
TreeNode<T> left; // Reference to left child
TreeNode<T> right; // Reference to right child
// Constructor
public TreeNode(T data) {
this.data = data;
this.left = null;
this.right = null;
}
// Constructor with children
public TreeNode(T data, TreeNode<T> left, TreeNode<T> right) {
this.data = data;
this.left = left;
this.right = right;
}
@Override
public String toString() {
return data.toString();
}
}
Generic Binary Tree Implementation
class BinaryTree<T extends Comparable<T>> {
private TreeNode<T> root;
public BinaryTree() {
this.root = null;
}
// Insert a new node
public void insert(T data) {
root = insertRecursive(root, data);
}
private TreeNode<T> insertRecursive(TreeNode<T> node, T data) {
// Base case: if tree is empty or reached leaf
if (node == null) {
return new TreeNode<>(data);
}
// Recursive case: traverse to find insertion point
int comparison = data.compareTo(node.data);
if (comparison < 0) {
node.left = insertRecursive(node.left, data);
} else if (comparison > 0) {
node.right = insertRecursive(node.right, data);
}
// If equal, do nothing (duplicate handling)
return node;
}
// Search for a value
public boolean search(T data) {
return searchRecursive(root, data);
}
private boolean searchRecursive(TreeNode<T> node, T data) {
// Base case: node is null or value found
if (node == null) {
return false;
}
if (node.data.equals(data)) {
return true;
}
// Recursive case: search in appropriate subtree
int comparison = data.compareTo(node.data);
if (comparison < 0) {
return searchRecursive(node.left, data);
} else {
return searchRecursive(node.right, data);
}
}
// Delete a node
public void delete(T data) {
root = deleteRecursive(root, data);
}
private TreeNode<T> deleteRecursive(TreeNode<T> node, T data) {
if (node == null) {
return null;
}
int comparison = data.compareTo(node.data);
if (comparison < 0) {
node.left = deleteRecursive(node.left, data);
} else if (comparison > 0) {
node.right = deleteRecursive(node.right, data);
} else {
// Node to delete found
// Case 1: Node is a leaf
if (node.left == null && node.right == null) {
return null;
}
// Case 2: Node has only one child
else if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
}
// Case 3: Node has two children
else {
TreeNode<T> successor = findMin(node.right);
node.data = successor.data;
node.right = deleteRecursive(node.right, successor.data);
}
}
return node;
}
private TreeNode<T> findMin(TreeNode<T> node) {
while (node.left != null) {
node = node.left;
}
return node;
}
// Get minimum value
public T getMin() {
if (root == null) return null;
return findMin(root).data;
}
// Get maximum value
public T getMax() {
if (root == null) return null;
return findMax(root).data;
}
private TreeNode<T> findMax(TreeNode<T> node) {
while (node.right != null) {
node = node.right;
}
return node;
}
// Get tree height
public int getHeight() {
return getHeightRecursive(root);
}
private int getHeightRecursive(TreeNode<T> node) {
if (node == null) {
return -1;
}
return Math.max(getHeightRecursive(node.left), getHeightRecursive(node.right)) + 1;
}
// Count total nodes
public int getSize() {
return getSizeRecursive(root);
}
private int getSizeRecursive(TreeNode<T> node) {
if (node == null) {
return 0;
}
return 1 + getSizeRecursive(node.left) + getSizeRecursive(node.right);
}
// Check if tree is empty
public boolean isEmpty() {
return root == null;
}
// Clear the tree
public void clear() {
root = null;
}
}
Tree Building and Visualization
1. Build Tree from Array
// Build tree from array of elements
public static <T extends Comparable<T>> BinaryTree<T> buildTree(T[] elements) {
BinaryTree<T> tree = new BinaryTree<>();
for (T element : elements) {
tree.insert(element);
}
return tree;
}
Generic Method Explanation
Why public static <T extends Comparable<T>> BinaryTree<T> buildTree(T[] elements)?
Let’s break down this method signature:
public static <T extends Comparable<T>> BinaryTree<T> buildTree(T[] elements)
│ │ │ │ │ │
│ │ │ │ │ └── Parameter type
│ │ │ │ └── Method name
│ │ │ └── Return type
│ │ └── Type parameter constraint
│ └── Type parameter declaration
└── Access modifier
1. <T extends Comparable<T>> - Type Parameter Declaration
// This declares a type parameter T that must be Comparable
<T extends Comparable<T>>
// Examples of valid types:
Integer (implements Comparable<Integer>)
String (implements Comparable<String>)
Double (implements Comparable<Double>)
// Examples of invalid types:
Object (doesn't implement Comparable)
CustomClass (unless it implements Comparable<CustomClass>)
2. Why extends Comparable<T>?
// We need Comparable because our BinaryTree uses compareTo() method
int comparison = data.compareTo(node.data); // This requires Comparable
// Without Comparable constraint, this would cause compilation error:
public static <T> BinaryTree<T> buildTree(T[] elements) { // ❌ Error!
// data.compareTo(node.data) - T doesn't have compareTo method
}
3. Why BinaryTree<T> as return type?
// Return type matches the type parameter
BinaryTree<T> tree = new BinaryTree<>(); // Creates tree of same type T
return tree; // Returns tree of type T
4. Why T[] elements as parameter?
// Parameter type matches the type parameter
T[] elements // Array of type T
for (T element : elements) { // Each element is of type T
tree.insert(element); // Insert T into BinaryTree<T>
}
Benefits of Our Generic Approach
1. Type Safety
// Compiler ensures type consistency
BinaryTree<Integer> tree = buildTree(numbers);
tree.insert(42); // ✅ Valid
tree.insert("hello"); // ❌ Compilation error
2. Code Reusability
// Same method works for multiple types
buildTree(new Integer[]{1, 2, 3}); // ✅ Integer tree
buildTree(new String[]{"a", "b", "c"}); // ✅ String tree
buildTree(new Double[]{1.1, 2.2, 3.3}); // ✅ Double tree
3. Performance
// No runtime type checking needed
// No boxing/unboxing overhead
// Direct method calls
4. Compile-time Error Detection
// Errors caught at compile time, not runtime
BinaryTree<String> tree = buildTree(numbers); // ❌ Compilation error
What Happens If You Don’t Use BinaryTree?
Scenario 1: Using Raw Type BinaryTree
// ❌ BAD: Using raw type
public static BinaryTree buildTree(Object[] elements) {
BinaryTree tree = new BinaryTree(); // Raw type
for (Object element : elements) {
tree.insert(element); // ❌ Type unsafe
}
return tree;
}
// Problems:
// 1. No type checking
// 2. Runtime errors possible
// 3. Compiler warnings
// 4. Unclear what type of tree you get back
Important Note: Raw Types DO Work!
// ✅ This actually works and compiles:
public static BinaryTree buildTree(Object[] elements) {
BinaryTree tree = new BinaryTree();
for (Object element : elements) {
tree.insert(element);
}
return tree;
}
// Usage:
Object[] data = {1, 2, 3, 4, 5};
BinaryTree tree = buildTree(data); // ✅ This works!
tree.search(3); // ✅ This works!
So Why Use Generics Then?
The raw type approach works but has risks:
- It works when data is consistent:
Object[] numbers = {1, 2, 3, 4, 5}; // ✅ All same type BinaryTree tree = buildTree(numbers); // ✅ Works fine - It also works when data is mixed (but with risks):
Object[] mixed = {1, "hello", 3.14}; // Mixed types BinaryTree tree = buildTree(mixed); // ✅ Compiles and runs // But may cause runtime errors when tree operations are performed
Example: Runtime Risk with Mixed Data
// Raw type method - accepts mixed data
public static BinaryTree buildTree(Object[] elements) {
BinaryTree tree = new BinaryTree();
for (Object element : elements) {
tree.insert(element);
}
return tree;
}
// Usage with mixed data:
Object[] mixed = {1, "hello", 3.14, true};
BinaryTree tree = buildTree(mixed); // ✅ Compiles successfully
// The tree is built, but operations may fail:
tree.search(1); // ✅ May work (Integer comparison)
tree.search("hello"); // ✅ May work (String comparison)
tree.search(3.14); // ❌ May cause ClassCastException
tree.search(true); // ❌ May cause ClassCastException
// The problem occurs when tree tries to compare different types:
// 1.compareTo("hello") → ClassCastException
// "hello".compareTo(3.14) → ClassCastException
Scenario 2: Using Specific Type
// ❌ BAD: Hard-coded to one type
public static BinaryTree<Integer> buildTree(Object[] elements) {
BinaryTree<Integer> tree = new BinaryTree<>();
for (Object element : elements) {
tree.insert((Integer) element); // ❌ Dangerous cast
}
return tree;
}
// Problems:
// 1. Runtime ClassCastException possible
// 2. Only works with Integer
// 3. Type casting overhead
Scenario 3: Using Wildcard
// ❌ BAD: Using wildcard
public static BinaryTree<?> buildTree(Object[] elements) {
BinaryTree<?> tree = new BinaryTree<>();
for (Object element : elements) {
// tree.insert(element); // ❌ Cannot insert into wildcard type
}
return tree;
}
// Problems:
// 1. Cannot insert elements
// 2. Useless return type
// 3. No type safety
Real Examples: When Raw Types Work vs Fail
✅ Raw Types Work (Consistent Data):
// This works perfectly fine:
public static BinaryTree buildTree(Object[] elements) {
BinaryTree tree = new BinaryTree();
for (Object element : elements) {
tree.insert(element);
}
return tree;
}
// Usage with consistent data:
Object[] numbers = {1, 2, 3, 4, 5};
BinaryTree tree = buildTree(numbers);
System.out.println(tree.search(3)); // ✅ Prints: true
System.out.println(tree.search(10)); // ✅ Prints: false
❌ Raw Types Fail (Mixed Data):
// Same method, but with mixed data:
Object[] mixed = {1, "hello", 3.14, true};
BinaryTree tree = buildTree(mixed);
// This will crash at runtime:
// java.lang.ClassCastException: java.lang.String cannot be cast to java.lang.Integer
Why Generics Are Better (Even Though Raw Types Work)
Raw Type Approach:
// ✅ Works, but risky
public static BinaryTree buildTree(Object[] elements) {
BinaryTree tree = new BinaryTree();
for (Object element : elements) {
tree.insert(element); // No type checking
}
return tree;
}
// Usage:
BinaryTree tree = buildTree(data);
// What type is this tree? Unknown!
// Will it crash? Maybe, depends on data!
Generic Approach:
// ✅ Works, and safe
public static <T extends Comparable<T>> BinaryTree<T> buildTree(T[] elements) {
BinaryTree<T> tree = new BinaryTree<>();
for (T element : elements) {
tree.insert(element); // Type checked
}
return tree;
}
// Usage:
BinaryTree<Integer> tree = buildTree(numbers);
// Clear: this is an Integer tree
// Guaranteed: won't crash due to type issues
Summary: Raw Types vs Generics
| Aspect | Raw Types | Generics |
|---|---|---|
| Does it work? | ✅ Yes (with consistent data) | ✅ Yes (always) |
| Type safety | ❌ No | ✅ Yes |
| Runtime errors | ❌ Possible | ✅ Prevented |
| Code clarity | ❌ Unclear types | ✅ Clear types |
| IDE support | ❌ Limited | ✅ Full |
| Best practice | ❌ Avoid | ✅ Recommended |
Bottom Line: Raw types do work for simple cases, but generics are safer and better because they prevent runtime errors and provide better code quality!
Tree Building Visualization
Building tree from array: [50, 30, 70, 20, 40]
Step 1: Insert 50 (Root)
50
Step 2: Insert 30 (30 < 50, go left)
50
/
30
Step 3: Insert 70 (70 > 50, go right)
50
/ \
30 70
Step 4: Insert 20 (20 < 50, 20 < 30, go left)
50
/ \
30 70
/
20
Step 5: Insert 40 (40 < 50, 40 > 30, go right)
50
/ \
30 70
/ \
20 40
Final Tree Structure:
50
/ \
30 70
/ \
20 40
2. Tree Structure Visualization
// Visualize tree structure with ASCII art
public static <T extends Comparable<T>> void visualizeTree(TreeNode<T> root) {
if (root == null) {
System.out.println("Empty tree");
return;
}
System.out.println("Tree Structure:");
printTree(root, "", true);
}
private static <T extends Comparable<T>> void printTree(TreeNode<T> node, String prefix, boolean isLeft) {
if (node == null) return;
System.out.println(prefix + (isLeft ? "└── " : "┌── ") + node.data);
printTree(node.left, prefix + (isLeft ? " " : "│ "), true);
printTree(node.right, prefix + (isLeft ? " " : "│ "), false);
}
Tree Structure Visualization Output
Tree Structure:
┌── 50
│ ├── 30
│ │ ├── 20
│ │ └── 40
│ └── 70
Visualization Explanation:
┌── Root node (50)
│ ├── Left subtree of 50 (30)
│ │ ├── Left child of 30 (20)
│ │ └── Right child of 30 (40)
│ └── Right subtree of 50 (70)
3. Level Order Visualization
// Print tree in level order (breadth-first)
public static <T extends Comparable<T>> void printLevelOrder(TreeNode<T> root) {
if (root == null) return;
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.offer(root);
System.out.println("Level Order Traversal:");
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
TreeNode<T> current = queue.poll();
System.out.print(current.data + " ");
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
System.out.println(); // New line for each level
}
}
Level Order Visualization Output
Level Order Traversal:
50
30 70
20 40
Visualization Explanation:
Level 0: 50 (Root)
Level 1: 30, 70 (Children of root)
Level 2: 20, 40 (Children of 30 and 70)
Queue State Visualization:
Initial: [50]
Level 1: [30, 70] (after processing 50)
Level 2: [20, 40] (after processing 30, 70)
Level 3: [] (after processing all children)
4. Complete Tree Visualization Class
class TreeVisualizer<T extends Comparable<T>> {
// Build tree from array
public static <T extends Comparable<T>> BinaryTree<T> buildTree(T[] elements) {
BinaryTree<T> tree = new BinaryTree<>();
for (T element : elements) {
tree.insert(element);
}
return tree;
}
// Visualize tree structure
public static <T extends Comparable<T>> void visualizeTree(TreeNode<T> root) {
if (root == null) {
System.out.println("Empty tree");
return;
}
System.out.println("Tree Structure:");
printTree(root, "", true);
}
private static <T extends Comparable<T>> void printTree(TreeNode<T> node, String prefix, boolean isLeft) {
if (node == null) return;
System.out.println(prefix + (isLeft ? "└── " : "┌── ") + node.data);
printTree(node.left, prefix + (isLeft ? " " : "│ "), true);
printTree(node.right, prefix + (isLeft ? " " : "│ "), false);
}
// Level-order visualization
public static <T extends Comparable<T>> void printLevelOrder(TreeNode<T> root) {
if (root == null) return;
Queue<TreeNode<T>> queue = new LinkedList<>();
queue.offer(root);
System.out.println("Level Order Traversal:");
while (!queue.isEmpty()) {
int levelSize = queue.size();
for (int i = 0; i < levelSize; i++) {
TreeNode<T> current = queue.poll();
System.out.print(current.data + " ");
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
System.out.println(); // New line for each level
}
}
}
Complete Visualization Example
Example Tree:
50
/ \
30 70
/ \
20 40
1. Tree Structure Output:
┌── 50
│ ├── 30
│ │ ├── 20
│ │ └── 40
│ └── 70
2. Level Order Output:
50
30 70
20 40
3. Tree Properties:
- Height: 1
- Size: 3 nodes
- Levels: 2
- Balanced: Yes
Basic Operations with Code and Visualizations
1. Insert Operation
// Insert a new element into the binary tree
public void insert(T data) {
root = insertRecursive(root, data);
}
private TreeNode<T> insertRecursive(TreeNode<T> node, T data) {
// Base case: if tree is empty or reached leaf
if (node == null) {
return new TreeNode<>(data);
}
// Recursive case: traverse to find insertion point
int comparison = data.compareTo(node.data);
if (comparison < 0) {
node.left = insertRecursive(node.left, data);
} else if (comparison > 0) {
node.right = insertRecursive(node.right, data);
}
// If equal, do nothing (duplicate handling)
return node;
}
Insert Operation Visualization
Inserting elements: [50, 30, 70, 20, 40]
Step 1: Insert 50 (Root)
50
Step 2: Insert 30 (30 < 50, go left)
50
/
30
Step 3: Insert 70 (70 > 50, go right)
50
/ \
30 70
Step 4: Insert 20 (20 < 50, 20 < 30, go left)
50
/ \
30 70
/
20
Step 5: Insert 40 (40 < 50, 40 > 30, go right)
50
/ \
30 70
/ \
20 40
Final Tree Structure:
50
/ \
30 70
/ \
20 40
2. Search Operation
// Search for an element in the binary tree
public boolean search(T data) {
return searchRecursive(root, data);
}
private boolean searchRecursive(TreeNode<T> node, T data) {
// Base case: node is null or value found
if (node == null) {
return false;
}
if (node.data.equals(data)) {
return true;
}
// Recursive case: search in appropriate subtree
int comparison = data.compareTo(node.data);
if (comparison < 0) {
return searchRecursive(node.left, data);
} else {
return searchRecursive(node.right, data);
}
}
Search Operation Visualization
Searching for element 40 in the tree:
Initial Tree:
50
/ \
30 70
/ \
20 40
Search Process:
Step 1: Start at root (50)
50 ← Check here
/ \
30 70
/ \
20 40
40 < 50? Yes → Go LEFT
Step 2: Check left child (30)
50
/ \
30 ← Check here
/ \
20 40
40 > 30? Yes → Go RIGHT
Step 3: Check right child (40)
50
/ \
30 70
/ \
20 40 ← Check here
40 == 40? Yes → FOUND!
Result: Element 40 found in 3 steps
3. Delete Operation
// Delete an element from the binary tree
public void delete(T data) {
root = deleteRecursive(root, data);
}
private TreeNode<T> deleteRecursive(TreeNode<T> node, T data) {
if (node == null) {
return null;
}
int comparison = data.compareTo(node.data);
if (comparison < 0) {
node.left = deleteRecursive(node.left, data);
} else if (comparison > 0) {
node.right = deleteRecursive(node.right, data);
} else {
// Node to delete found
// Case 1: Node is a leaf
if (node.left == null && node.right == null) {
return null;
}
// Case 2: Node has only one child
else if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
}
// Case 3: Node has two children
else {
TreeNode<T> successor = findMin(node.right);
node.data = successor.data;
node.right = deleteRecursive(node.right, successor.data);
}
}
return node;
}
private TreeNode<T> findMin(TreeNode<T> node) {
while (node.left != null) {
node = node.left;
}
return node;
}
Delete Operation Visualization
Case 1: Delete Leaf Node (20)
Before deletion:
50
/ \
30 70
/ \
20 40
After deletion:
50
/ \
30 70
\
40
Case 2: Delete Node with One Child (70)
Before deletion:
50
/ \
30 70
\
80
After deletion:
50
/ \
30 80
Case 3: Delete Node with Two Children (30)
Before deletion:
50
/ \
30 70
/ \
20 40
Step 1: Find successor (minimum in right subtree = 40)
50
/ \
30 70
/ \
20 40 ← Successor
Step 2: Replace 30 with 40
50
/ \
40 70
/ \
20 40
Step 3: Delete the duplicate 40 (leaf node)
50
/ \
40 70
/
20
Final result:
50
/ \
40 70
/
20
4. Get Minimum/Maximum Operation
// Get minimum value in the tree
public T getMin() {
if (root == null) return null;
return findMin(root).data;
}
// Get maximum value in the tree
public T getMax() {
if (root == null) return null;
return findMax(root).data;
}
private TreeNode<T> findMax(TreeNode<T> node) {
while (node.right != null) {
node = node.right;
}
return node;
}
Min/Max Operation Visualization
Finding minimum in the tree:
50
/ \
30 70
/ \
20 40
Path to minimum:
50 → 30 → 20 ← Minimum (leftmost node)
Finding maximum in the tree:
50
/ \
30 70
/ \
20 40
Path to maximum:
50 → 70 ← Maximum (rightmost node)
5. Get Height Operation
// Get the height of the tree
public int getHeight() {
return getHeightRecursive(root);
}
private int getHeightRecursive(TreeNode<T> node) {
if (node == null) {
return -1;
}
return Math.max(getHeightRecursive(node.left), getHeightRecursive(node.right)) + 1;
}
Height Calculation Visualization
Calculating height of the tree:
50
/ \
30 70
/ \
20 40
Height calculation:
- Node 50: max(height(30), height(70)) + 1
- Node 30: max(height(20), height(40)) + 1 = max(0, 0) + 1 = 1
- Node 70: height = 0 (leaf)
- Node 20: height = 0 (leaf)
- Node 40: height = 0 (leaf)
Final height: max(1, 0) + 1 = 2
6. Get Size Operation
// Get the total number of nodes in the tree
public int getSize() {
return getSizeRecursive(root);
}
private int getSizeRecursive(TreeNode<T> node) {
if (node == null) {
return 0;
}
return 1 + getSizeRecursive(node.left) + getSizeRecursive(node.right);
}
Size Calculation Visualization
Counting nodes in the tree:
50
/ \
30 70
/ \
20 40
Size calculation:
- Node 50: 1 + size(30) + size(70)
- Node 30: 1 + size(20) + size(40) = 1 + 1 + 1 = 3
- Node 70: 1 + size(null) + size(null) = 1 + 0 + 0 = 1
- Node 20: 1 + size(null) + size(null) = 1 + 0 + 0 = 1
- Node 40: 1 + size(null) + size(null) = 1 + 0 + 0 = 1
Total size: 1 + 3 + 1 = 5 nodes
Complete Example Demo
public class BinaryTreeDemo {
public static void main(String[] args) {
// Create a binary tree with integers
BinaryTree<Integer> intTree = new BinaryTree<>();
// Insert elements
int[] elements = {50, 30, 70, 20, 40, 60, 80, 10, 25, 35, 45, 55, 65, 75, 85};
System.out.println("=== Building Binary Tree ===");
for (int element : elements) {
intTree.insert(element);
System.out.println("Inserted: " + element);
}
// Visualize the tree
System.out.println("\n=== Tree Visualization ===");
TreeVisualizer.visualizeTree(intTree.root);
// Level order traversal
System.out.println("\n=== Level Order Traversal ===");
TreeVisualizer.printLevelOrder(intTree.root);
// Basic operations
System.out.println("\n=== Basic Operations ===");
System.out.println("Tree size: " + intTree.getSize());
System.out.println("Tree height: " + intTree.getHeight());
System.out.println("Minimum value: " + intTree.getMin());
System.out.println("Maximum value: " + intTree.getMax());
System.out.println("Is empty: " + intTree.isEmpty());
// Search operations
System.out.println("\n=== Search Operations ===");
System.out.println("Search for 40: " + intTree.search(40));
System.out.println("Search for 90: " + intTree.search(90));
// Delete operations
System.out.println("\n=== Delete Operations ===");
System.out.println("Deleting 30...");
intTree.delete(30);
TreeVisualizer.visualizeTree(intTree.root);
// String tree example
System.out.println("\n=== String Tree Example ===");
BinaryTree<String> stringTree = new BinaryTree<>();
String[] words = {"apple", "banana", "cherry", "date", "elderberry"};
for (String word : words) {
stringTree.insert(word);
}
TreeVisualizer.visualizeTree(stringTree.root);
}
}
Types of Binary Trees
1. Full Binary Tree
Every node has either 0 or 2 children.
Example:
1
/ \
2 3
/ \
4 5
Properties:
- All internal nodes have exactly 2 children
- Leaf nodes have 0 children
- Number of nodes = 2^h - 1 (where h is height)
2. Complete Binary Tree
All levels are filled except possibly the last level, which is filled from left to right.
Example:
1
/ \
2 3
/ \ /
4 5 6
Properties:
- All levels except last are completely filled
- Last level is filled from left to right
- Used in heap data structure
3. Perfect Binary Tree
All internal nodes have 2 children and all leaves are at the same level.
Example:
1
/ \
2 3
/ \ / \
4 5 6 7
Properties:
- All internal nodes have 2 children
- All leaves at same level
- Height = log₂(n+1)
4. Balanced Binary Tree
Height difference between left and right subtrees is at most 1.
Example:
1
/ \
2 3
/ \
4 5
Properties:
- |height(left) - height(right)| ≤ 1
- Ensures O(log n) operations
- AVL trees and Red-Black trees are balanced
Tree Traversal Methods
1. Inorder Traversal (Left → Root → Right)
public void inorderTraversal(TreeNode root) {
if (root == null) return; // Base case
inorderTraversal(root.left); // Visit left subtree
System.out.print(root.val + " "); // Visit current node
inorderTraversal(root.right); // Visit right subtree
}
Visualization of Inorder Traversal
Example Tree:
1
/ \
2 3
/ \ \
4 5 6
Inorder Traversal: 4 → 2 → 5 → 1 → 3 → 6
Step-by-Step Process:
Step 1: Start at root(1)
- Go left to node(2)
- Go left to node(4)
- Print 4 (leftmost leaf)
Step 2: Back to node(2)
- Print 2 (left subtree done)
Step 3: Go right to node(5)
- Print 5 (right subtree of 2)
Step 4: Back to root(1)
- Print 1 (left subtree done)
Step 5: Go right to node(3)
- Print 3 (no left child)
Step 6: Go right to node(6)
- Print 6 (rightmost leaf)
Result: 4 2 5 1 3 6
2. Preorder Traversal (Root → Left → Right)
public void preorderTraversal(TreeNode root) {
if (root == null) return; // Base case
System.out.print(root.val + " "); // Visit current node first
preorderTraversal(root.left); // Visit left subtree
preorderTraversal(root.right); // Visit right subtree
}
Visualization of Preorder Traversal
Example Tree:
1
/ \
2 3
/ \ \
4 5 6
Preorder Traversal: 1 → 2 → 4 → 5 → 3 → 6
Step-by-Step Process:
Step 1: Start at root(1)
- Print 1 immediately
Step 2: Go left to node(2)
- Print 2 immediately
Step 3: Go left to node(4)
- Print 4 immediately
Step 4: Back to node(2), go right to node(5)
- Print 5 immediately
Step 5: Back to root(1), go right to node(3)
- Print 3 immediately
Step 6: Go right to node(6)
- Print 6 immediately
Result: 1 2 4 5 3 6
3. Postorder Traversal (Left → Right → Root)
public void postorderTraversal(TreeNode root) {
if (root == null) return; // Base case
postorderTraversal(root.left); // Visit left subtree
postorderTraversal(root.right); // Visit right subtree
System.out.print(root.val + " "); // Visit current node last
}
Visualization of Postorder Traversal
Example Tree:
1
/ \
2 3
/ \ \
4 5 6
Postorder Traversal: 4 → 5 → 2 → 6 → 3 → 1
Step-by-Step Process:
Step 1: Start at root(1)
- Go left to node(2)
- Go left to node(4)
- Print 4 (no children)
Step 2: Back to node(2), go right to node(5)
- Print 5 (no children)
Step 3: Back to node(2)
- Print 2 (both children visited)
Step 4: Back to root(1), go right to node(3)
- Go right to node(6)
- Print 6 (no children)
Step 5: Back to node(3)
- Print 3 (both children visited)
Step 6: Back to root(1)
- Print 1 (both children visited)
Result: 4 5 2 6 3 1
4. Level Order Traversal (Breadth-First)
import java.util.*;
public void levelOrderTraversal(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode current = queue.poll();
System.out.print(current.val + " ");
if (current.left != null) {
queue.offer(current.left);
}
if (current.right != null) {
queue.offer(current.right);
}
}
}
Visualization of Level Order Traversal
Example Tree:
1
/ \
2 3
/ \ \
4 5 6
Level Order Traversal: 1 → 2 → 3 → 4 → 5 → 6
Queue State Visualization:
Initial: [1]
Level 1: [2, 3] (after processing 1)
Level 2: [4, 5, 6] (after processing 2, 3)
Level 3: [] (after processing 4, 5, 6)
Step-by-Step Process:
Step 1: Queue = [1], print 1, add [2, 3]
Step 2: Queue = [2, 3], print 2, add [4, 5]
Step 3: Queue = [3, 4, 5], print 3, add [6]
Step 4: Queue = [4, 5, 6], print 4
Step 5: Queue = [5, 6], print 5
Step 6: Queue = [6], print 6
Step 7: Queue = [], done
Result: 1 2 3 4 5 6
Common Binary Tree Operations
1. Calculate Tree Height
public int getHeight(TreeNode root) {
if (root == null) {
return -1; // Empty tree has height -1
}
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return Math.max(leftHeight, rightHeight) + 1;
}
Visualization of Height Calculation
Example Tree:
1
/ \
2 3
/ \ \
4 5 6
Height Calculation Process:
- Node 1: max(height(2), height(3)) + 1
- Node 2: max(height(4), height(5)) + 1 = max(0, 0) + 1 = 1
- Node 3: max(height(null), height(6)) + 1 = max(-1, 0) + 1 = 1
- Node 4: height = 0 (leaf)
- Node 5: height = 0 (leaf)
- Node 6: height = 0 (leaf)
Final Result: max(1, 1) + 1 = 2
2. Count Total Nodes
public int countNodes(TreeNode root) {
if (root == null) {
return 0; // Base case
}
return 1 + countNodes(root.left) + countNodes(root.right);
}
3. Count Leaf Nodes
public int countLeaves(TreeNode root) {
if (root == null) {
return 0; // Base case
}
// If it's a leaf node
if (root.left == null && root.right == null) {
return 1;
}
return countLeaves(root.left) + countLeaves(root.right);
}
4. Check if Tree is Balanced
public boolean isBalanced(TreeNode root) {
return checkBalance(root) != -1;
}
private int checkBalance(TreeNode root) {
if (root == null) {
return 0; // Base case
}
int leftHeight = checkBalance(root.left);
if (leftHeight == -1) return -1; // Left subtree unbalanced
int rightHeight = checkBalance(root.right);
if (rightHeight == -1) return -1; // Right subtree unbalanced
if (Math.abs(leftHeight - rightHeight) > 1) {
return -1; // Current node unbalanced
}
return Math.max(leftHeight, rightHeight) + 1;
}
Binary Search Tree (BST)
Definition
A Binary Search Tree is a binary tree where for each node:
- All nodes in the left subtree have values less than the node’s value
- All nodes in the right subtree have values greater than the node’s value
BST Implementation
class BinarySearchTree {
private TreeNode root;
public BinarySearchTree() {
this.root = null;
}
// Insert operation
public void insert(int val) {
root = insertRecursive(root, val);
}
private TreeNode insertRecursive(TreeNode node, int val) {
if (node == null) {
return new TreeNode(val);
}
if (val < node.val) {
node.left = insertRecursive(node.left, val);
} else if (val > node.val) {
node.right = insertRecursive(node.right, val);
}
return node;
}
// Search operation
public boolean search(int val) {
return searchRecursive(root, val);
}
private boolean searchRecursive(TreeNode node, int val) {
if (node == null) {
return false;
}
if (node.val == val) {
return true;
}
if (val < node.val) {
return searchRecursive(node.left, val);
} else {
return searchRecursive(node.right, val);
}
}
// Delete operation
public void delete(int val) {
root = deleteRecursive(root, val);
}
private TreeNode deleteRecursive(TreeNode node, int val) {
if (node == null) {
return null;
}
if (val < node.val) {
node.left = deleteRecursive(node.left, val);
} else if (val > node.val) {
node.right = deleteRecursive(node.right, val);
} else {
// Node to delete found
// Case 1: Node is a leaf
if (node.left == null && node.right == null) {
return null;
}
// Case 2: Node has only one child
else if (node.left == null) {
return node.right;
} else if (node.right == null) {
return node.left;
}
// Case 3: Node has two children
else {
TreeNode successor = findMin(node.right);
node.val = successor.val;
node.right = deleteRecursive(node.right, successor.val);
}
}
return node;
}
private TreeNode findMin(TreeNode node) {
while (node.left != null) {
node = node.left;
}
return node;
}
}
BST Operations Visualization
Example BST:
5
/ \
3 7
/ \ \
1 4 9
Insert 2:
5
/ \
3 7
/ \ \
1 4 9
\
2
Delete 3:
5
/ \
4 7
/ \
1 9
\
2
Time Complexity Analysis
The performance characteristics of binary trees are best understood through complexity analysis. As demonstrated in the complexity comparison chart above, binary trees provide logarithmic time complexity for most operations, making them dramatically more efficient than linear data structures for large datasets.
Basic Operations
| Operation | Average Case | Worst Case |
|---|---|---|
| Search | O(log n) | O(n) |
| Insert | O(log n) | O(n) |
| Delete | O(log n) | O(n) |
| Traversal | O(n) | O(n) |
Space Complexity
| Operation | Space Complexity |
|---|---|
| Recursive Traversal | O(h) - height of tree |
| Iterative Traversal | O(w) - width of tree |
| Level Order | O(w) - maximum width |
Practical Applications
1. Expression Trees
class ExpressionNode {
String value;
ExpressionNode left, right;
public ExpressionNode(String value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class ExpressionTree {
public int evaluate(ExpressionNode root) {
if (root == null) return 0;
// If leaf node (operand)
if (root.left == null && root.right == null) {
return Integer.parseInt(root.value);
}
// Evaluate left and right subtrees
int leftVal = evaluate(root.left);
int rightVal = evaluate(root.right);
// Apply operator
switch (root.value) {
case "+": return leftVal + rightVal;
case "-": return leftVal - rightVal;
case "*": return leftVal * rightVal;
case "/": return leftVal / rightVal;
default: return 0;
}
}
}
Example Expression Tree
Expression: (3 + 4) * 2
Tree Structure:
*
/ \
+ 2
/ \
3 4
Evaluation:
- Evaluate left subtree: 3 + 4 = 7
- Evaluate right subtree: 2
- Apply operator: 7 * 2 = 14
2. File System Tree
class FileNode {
String name;
boolean isDirectory;
List<FileNode> children;
public FileNode(String name, boolean isDirectory) {
this.name = name;
this.isDirectory = isDirectory;
this.children = new ArrayList<>();
}
}
class FileSystemTree {
public void printTree(FileNode root, String indent) {
if (root == null) return;
System.out.println(indent + (root.isDirectory ? "📁 " : "📄 ") + root.name);
if (root.isDirectory) {
for (FileNode child : root.children) {
printTree(child, indent + " ");
}
}
}
}
3. Decision Trees
class DecisionNode {
String question;
DecisionNode yesChild, noChild;
String result; // null for internal nodes
public DecisionNode(String question) {
this.question = question;
this.yesChild = null;
this.noChild = null;
this.result = null;
}
public DecisionNode(String result) {
this.question = null;
this.yesChild = null;
this.noChild = null;
this.result = result;
}
}
class DecisionTree {
public String makeDecision(DecisionNode root) {
if (root == null) return null;
// If leaf node, return result
if (root.result != null) {
return root.result;
}
// Ask question and traverse accordingly
// This is a simplified version - in practice, you'd get user input
boolean answer = askQuestion(root.question);
if (answer) {
return makeDecision(root.yesChild);
} else {
return makeDecision(root.noChild);
}
}
private boolean askQuestion(String question) {
// Simplified - in practice, this would get user input
System.out.println(question + " (y/n)");
return true; // Placeholder
}
}
Practice Problems
Problem 1: Validate Binary Search Tree
class Solution {
public boolean isValidBST(TreeNode root) {
return isValidBSTHelper(root, Long.MIN_VALUE, Long.MAX_VALUE);
}
private boolean isValidBSTHelper(TreeNode node, long min, long max) {
if (node == null) return true;
if (node.val <= min || node.val >= max) {
return false;
}
return isValidBSTHelper(node.left, min, node.val) &&
isValidBSTHelper(node.right, node.val, max);
}
}
Problem 2: Lowest Common Ancestor
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if (left != null && right != null) {
return root;
}
return left != null ? left : right;
}
}
Problem 3: Serialize and Deserialize Binary Tree
class Codec {
public String serialize(TreeNode root) {
if (root == null) return "null";
return root.val + "," + serialize(root.left) + "," + serialize(root.right);
}
public TreeNode deserialize(String data) {
Queue<String> queue = new LinkedList<>(Arrays.asList(data.split(",")));
return deserializeHelper(queue);
}
private TreeNode deserializeHelper(Queue<String> queue) {
String val = queue.poll();
if ("null".equals(val)) return null;
TreeNode node = new TreeNode(Integer.parseInt(val));
node.left = deserializeHelper(queue);
node.right = deserializeHelper(queue);
return node;
}
}
Practice Problem: Two Sum in Binary Search Tree
Problem Description
Given a Binary Search Tree and a target sum, find all pairs of nodes whose values sum up to the target. Return the pairs as a list of arrays.
Examples
Input:
5
/ \
3 7
/ \ \
1 4 9
target = 8
Output: [[1,7], [3,5]]
Explanation:
- 1 + 7 = 8
- 3 + 5 = 8
Input:
10
/ \
5 15
/ \ \
3 7 18
target = 12
Output: [[5,7]]
Explanation:
- 5 + 7 = 12
Solution Approach
This problem combines Binary Search Tree traversal with Hash Table for efficient lookup.
Inorder Traversal + Hash Table
class Solution {
public List<List<Integer>> findPairs(TreeNode root, int target) {
List<List<Integer>> result = new ArrayList<>();
Set<Integer> set = new HashSet<>();
// Inorder traversal to visit nodes in sorted order
inorderTraversal(root, target, set, result);
return result;
}
private void inorderTraversal(TreeNode node, int target, Set<Integer> set, List<List<Integer>> result) {
if (node == null) return;
// Traverse left subtree
inorderTraversal(node.left, target, set, result);
// Check if complement exists in hash table
int complement = target - node.val;
if (set.contains(complement)) {
result.add(Arrays.asList(complement, node.val));
}
// Add current node to hash table
set.add(node.val);
// Traverse right subtree
inorderTraversal(node.right, target, set, result);
}
}
Step-by-Step Visualization
Tree: 5
/ \
3 7
/ \ \
1 4 9
Target: 8
Step-by-Step Process:
Step 1: Inorder traversal starts
- Go to leftmost node (1)
- Check: complement = 8 - 1 = 7
- Hash table: {} (empty)
- Add 1 to hash table: {1}
Step 2: Visit node 3
- Check: complement = 8 - 3 = 5
- Hash table: {1}
- 5 not found, add 3: {1, 3}
Step 3: Visit node 4
- Check: complement = 8 - 4 = 4
- Hash table: {1, 3}
- 4 not found, add 4: {1, 3, 4}
Step 4: Visit node 5
- Check: complement = 8 - 5 = 3
- Hash table: {1, 3, 4}
- 3 found! Add pair [3, 5]
- Add 5: {1, 3, 4, 5}
Step 5: Visit node 7
- Check: complement = 8 - 7 = 1
- Hash table: {1, 3, 4, 5}
- 1 found! Add pair [1, 7]
- Add 7: {1, 3, 4, 5, 7}
Step 6: Visit node 9
- Check: complement = 8 - 9 = -1
- Hash table: {1, 3, 4, 5, 7}
- -1 not found, add 9: {1, 3, 4, 5, 7, 9}
Result: [[3,5], [1,7]]
Complexity Analysis
- Time Complexity: O(n) - single inorder traversal
- Space Complexity: O(n) - hash table storage
- Advantages: Single pass, efficient O(1) lookup
- Disadvantages: Extra space for hash table
Follow-up Questions
- What if the tree is not a BST?
- Hash table approach still works
- Two pointers approach fails (array not sorted)
- What if we need to find all possible pairs (including duplicates)?
- Use HashMap<Integer, Integer> to count frequencies
- Handle cases where node.val == target/2
Related Problems
- Two Sum (Array version)
- Find Mode in Binary Search Tree
- Convert BST to Greater Tree
- Two Sum IV - Input is a BST
This problem demonstrates how combining different data structures (Binary Search Tree + Hash Table) can lead to efficient solutions for complex problems.
Summary
- Binary Tree: Hierarchical structure with at most 2 children per node
- Traversal Methods: Inorder, Preorder, Postorder, Level Order
- BST Properties: Left subtree < Root < Right subtree
- Common Operations: Insert, Delete, Search, Height calculation
- Applications: Expression trees, file systems, decision trees
- Time Complexity: O(log n) average, O(n) worst case for BST operations
Binary trees are fundamental data structures that provide efficient organization and retrieval of hierarchical data, making them essential for many algorithms and applications in computer science.