Binary Tree vs Binary Search Tree: Comprehensive Comparison
Overview
This document provides a detailed comparison between Binary Trees (BT) and Binary Search Trees (BST), including their structures, operations, performance characteristics, and practical applications. We’ll explore the key differences and when to use each data structure.
Basic Definitions
Binary Tree (BT)
A hierarchical data structure where each node has at most two children, with no ordering constraints.
Binary Search Tree (BST)
A binary tree with strict ordering constraints: left subtree values < root value < right subtree values.
Structural Comparison
Visual Representation
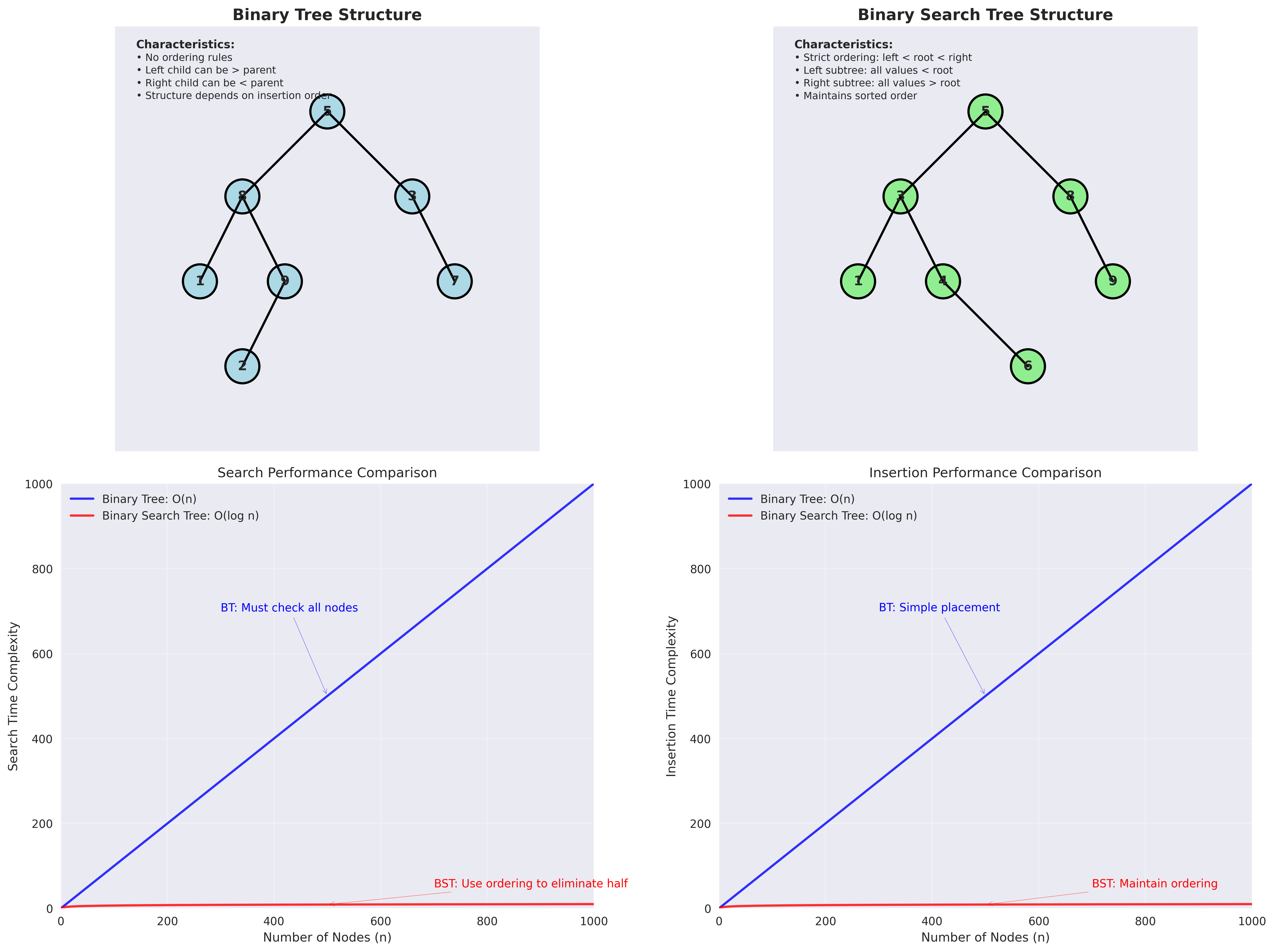
Figure: Comprehensive comparison of Binary Tree vs Binary Search Tree structures and performance characteristics. The top row shows structural differences, while the bottom row demonstrates performance comparisons.
Binary Tree Structure
5
/ \
8 3
/ \ \
1 9 7
/
2
Characteristics:
- No ordering rules
- Left child can be > parent
- Right child can be < parent
- Structure depends on insertion order
Binary Search Tree Structure
5
/ \
3 8
/ \ \
1 4 9
\
6
Characteristics:
- Strict ordering: left < root < right
- Left subtree: all values < root
- Right subtree: all values > root
- Maintains sorted order
Implementation Comparison
Node Structure
Both use the same basic node structure:
class Node<T> {
T data;
Node<T> left;
Node<T> right;
public Node(T data) {
this.data = data;
this.left = null;
this.right = null;
}
}
Insertion Operations
Binary Tree Insertion
class BinaryTree<T> {
Node<T> root;
public void insert(T data) {
root = insertRec(root, data);
}
private Node<T> insertRec(Node<T> root, T data) {
if (root == null) {
return new Node<>(data);
}
// Simple insertion strategy: fill left, then right
if (root.left == null) {
root.left = insertRec(root.left, data);
} else if (root.right == null) {
root.right = insertRec(root.right, data);
} else {
// If both children exist, insert into left subtree
root.left = insertRec(root.left, data);
}
return root;
}
}
Binary Search Tree Insertion
class BinarySearchTree<T extends Comparable<T>> {
Node<T> root;
public void insert(T data) {
root = insertRec(root, data);
}
private Node<T> insertRec(Node<T> root, T data) {
if (root == null) {
return new Node<>(data);
}
// Follow BST ordering rules
if (data.compareTo(root.data) < 0) {
root.left = insertRec(root.left, data);
} else if (data.compareTo(root.data) > 0) {
root.right = insertRec(root.right, data);
}
// Equal values can be handled as needed
return root;
}
}
Search Operations Comparison
Binary Tree Search
class BinaryTree<T> {
public boolean search(T data) {
return searchRec(root, data);
}
private boolean searchRec(Node<T> root, T data) {
if (root == null) return false;
if (root.data.equals(data)) return true;
// Must search both subtrees
return searchRec(root.left, data) || searchRec(root.right, data);
}
}
Binary Search Tree Search
class BinarySearchTree<T extends Comparable<T>> {
public boolean search(T data) {
return searchRec(root, data);
}
private boolean searchRec(Node<T> root, T data) {
if (root == null) return false;
if (root.data.equals(data)) return true;
// Use ordering to eliminate one subtree
if (data.compareTo(root.data) < 0) {
return searchRec(root.left, data); // Only search left
} else {
return searchRec(root.right, data); // Only search right
}
}
}
Performance Analysis
Time Complexity Comparison
| Operation | Binary Tree | Binary Search Tree |
|---|---|---|
| Insertion | O(n) | O(log n) |
| Search | O(n) | O(log n) |
| Deletion | O(n) | O(log n) |
| Traversal | O(n) | O(n) |
| Min/Max | O(n) | O(log n) |
Space Complexity
Both structures have the same space complexity:
- Worst Case: O(n) - when tree becomes a linked list
- Best Case: O(log n) - when tree is balanced
Performance Visualization
The comprehensive comparison chart above shows both structural differences and performance characteristics. For detailed performance analysis, see also:
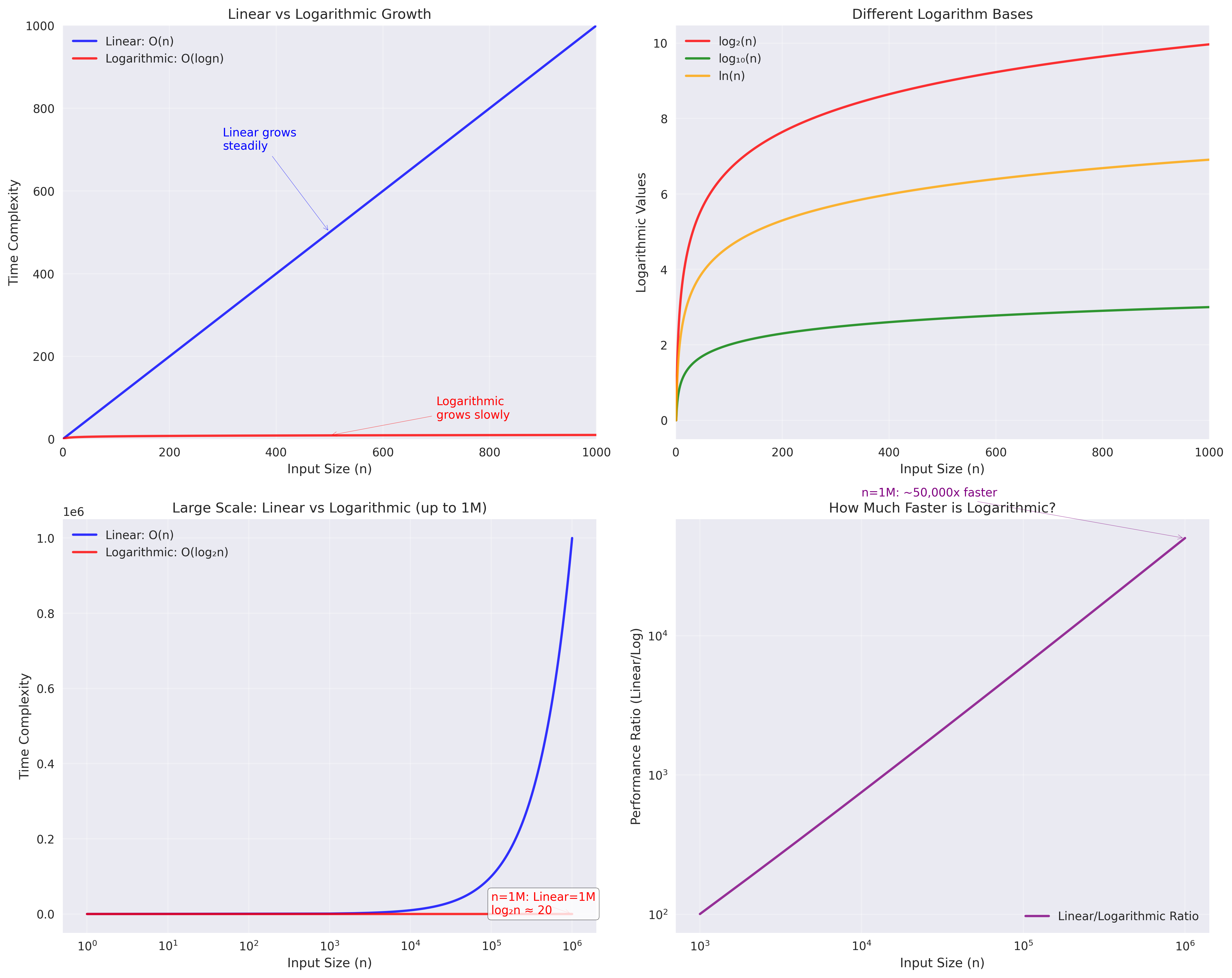
Figure: Performance comparison showing the dramatic difference between linear O(n) and logarithmic O(log n) operations.
Detailed Performance Analysis
The performance differences between Binary Trees and Binary Search Trees are clearly illustrated in the comparison chart above. Let’s examine the search and insertion processes in detail:
Search Performance Comparison
Binary Tree Search Process
Searching for value 7 in BT:
5
/ \
8 3
/ \ \
1 9 7
/
2
Search Steps:
1. Check root (5) → not found
2. Check left subtree (8) → not found
3. Check left subtree of 8 (1) → not found
4. Check right subtree of 8 (9) → not found
5. Check left subtree of 9 (2) → not found
6. Check right subtree of 5 (3) → not found
7. Check right subtree of 3 (7) → found!
Total comparisons: 7 (worst case: n)
Binary Search Tree Search Process
Searching for value 7 in BST:
5
/ \
3 8
/ \ \
1 4 9
\
6
Search Steps:
1. Check root (5) → 7 > 5, go right
2. Check node (8) → 7 < 8, go left
3. Check node (6) → 7 > 6, go right
4. Found 7!
Total comparisons: 4 (worst case: log n)
Insertion Performance Comparison
Binary Tree Insertion
// Insertion strategy affects tree shape
BinaryTree<Integer> bt = new BinaryTree<>();
bt.insert(5); // Root
bt.insert(3); // Left child
bt.insert(8); // Right child
bt.insert(1); // Left of left
bt.insert(4); // Right of left
bt.insert(7); // Left of right
bt.insert(9); // Right of right
// Result: balanced tree by chance
// But no guarantee of balance
Binary Search Tree Insertion
// Insertion maintains ordering
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
bst.insert(5); // Root
bst.insert(3); // Left (3 < 5)
bst.insert(8); // Right (8 > 5)
bst.insert(1); // Left of left (1 < 3)
bst.insert(4); // Right of left (4 > 3, 4 < 5)
bst.insert(7); // Left of right (7 < 8, 7 > 5)
bst.insert(9); // Right of right (9 > 8)
// Result: automatically sorted
// But may become unbalanced
Practical Applications
Binary Tree Applications
1. Expression Trees
// Mathematical expression: (3 + 4) * 2
class ExpressionTree {
class Node {
String value; // Operator or operand
Node left, right;
}
// Tree structure:
// *
// / \
// + 2
// / \
// 3 4
public int evaluate(Node root) {
if (root == null) return 0;
// If leaf node (operand)
if (root.left == null && root.right == null) {
return Integer.parseInt(root.value);
}
// Evaluate subtrees
int leftVal = evaluate(root.left);
int rightVal = evaluate(root.right);
// Apply operator
switch (root.value) {
case "+": return leftVal + rightVal;
case "*": return leftVal * rightVal;
default: return 0;
}
}
}
2. File System Trees
class FileSystemTree {
class Node {
String name;
boolean isDirectory;
Node left, right; // Child files/folders
}
// Tree structure:
// 📁 Root
// / \
// 📁 Docs 📁 Pictures
// / \ / \
// 📄 A 📄 B 📄 C 📄 D
}
3. Decision Trees
class DecisionTree {
class Node {
String question;
Node left, right; // Yes/No branches
}
// Tree structure:
// Is it raining?
// / \
// Yes No
// | |
// Stay inside Go outside
}
Binary Search Tree Applications
1. Database Indexing
class DatabaseIndex {
class User {
int id;
String name;
String email;
}
BinarySearchTree<Integer> idIndex = new BinarySearchTree<>();
public void addUser(User user) {
idIndex.insert(user.id);
}
public boolean findUser(int id) {
return idIndex.search(id); // O(log n) lookup
}
}
2. Dictionary Implementation
class Dictionary {
BinarySearchTree<String> words = new BinarySearchTree<>();
public void addWord(String word) {
words.insert(word.toLowerCase());
}
public boolean containsWord(String word) {
return words.search(word.toLowerCase()); // O(log n) lookup
}
public List<String> getWordsInRange(String start, String end) {
// In-order traversal gives sorted words
return words.inOrderTraversal().stream()
.filter(word -> word.compareTo(start) >= 0 &&
word.compareTo(end) <= 0)
.collect(Collectors.toList());
}
}
3. Priority Queue
class PriorityQueue<T extends Comparable<T>> {
BinarySearchTree<T> tree = new BinarySearchTree<>();
public void enqueue(T item) {
tree.insert(item);
}
public T dequeue() {
T min = tree.findMin(); // O(log n)
tree.delete(min);
return min;
}
public T peek() {
return tree.findMin(); // O(log n)
}
}
Memory Usage Comparison
Binary Tree Memory
// Memory layout example
BinaryTree<Integer> bt = new BinaryTree<>();
bt.insert(5);
bt.insert(8);
bt.insert(3);
// Memory allocation:
// Node 5: [data=5, left=ref_to_8, right=ref_to_3]
// Node 8: [data=8, left=null, right=null]
// Node 3: [data=3, left=null, right=null]
Binary Search Tree Memory
// Memory layout example
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
bst.insert(5);
bst.insert(3);
bst.insert(8);
// Memory allocation:
// Node 5: [data=5, left=ref_to_3, right=ref_to_8]
// Node 3: [data=3, left=null, right=null]
// Node 8: [data=8, left=null, right=null]
// Same memory usage, different organization
When to Use Each Structure
Choose Binary Tree When:
- No ordering requirements
- Hierarchical data representation
- Expression evaluation
- File system modeling
- Decision tree algorithms
- Simple tree operations
Choose Binary Search Tree When:
- Sorted data requirements
- Fast search operations
- Database indexing
- Dictionary implementation
- Priority queue
- Range queries
Code Examples with Visualization
Binary Tree Implementation with Visualization
class BinaryTree<T> {
Node<T> root;
public void insert(T data) {
root = insertRec(root, data);
}
private Node<T> insertRec(Node<T> root, T data) {
if (root == null) {
return new Node<>(data);
}
// Simple insertion: fill left, then right
if (root.left == null) {
root.left = insertRec(root.left, data);
} else if (root.right == null) {
root.right = insertRec(root.right, data);
} else {
root.left = insertRec(root.left, data);
}
return root;
}
public void printTree() {
printTreeRec(root, 0);
}
private void printTreeRec(Node<T> root, int depth) {
if (root == null) return;
// Print right subtree
printTreeRec(root.right, depth + 1);
// Print current node
String indent = " ".repeat(depth);
System.out.println(indent + root.data);
// Print left subtree
printTreeRec(root.left, depth + 1);
}
}
Binary Search Tree Implementation with Visualization
class BinarySearchTree<T extends Comparable<T>> {
Node<T> root;
public void insert(T data) {
root = insertRec(root, data);
}
private Node<T> insertRec(Node<T> root, T data) {
if (root == null) {
return new Node<>(data);
}
// Follow BST ordering
if (data.compareTo(root.data) < 0) {
root.left = insertRec(root.left, data);
} else if (data.compareTo(root.data) > 0) {
root.right = insertRec(root.right, data);
}
return root;
}
public void printTree() {
printTreeRec(root, 0);
}
private void printTreeRec(Node<T> root, int depth) {
if (root == null) return;
// Print right subtree
printTreeRec(root.right, depth + 1);
// Print current node
String indent = " ".repeat(depth);
System.out.println(indent + root.data);
// Print left subtree
printTreeRec(root.left, depth + 1);
}
public T findMin() {
if (root == null) return null;
Node<T> current = root;
while (current.left != null) {
current = current.left;
}
return current.data;
}
public T findMax() {
if (root == null) return null;
Node<T> current = root;
while (current.right != null) {
current = current.right;
}
return current.data;
}
}
Performance Testing
Test Code
public class TreePerformanceTest {
public static void main(String[] args) {
int n = 10000;
// Test Binary Tree
BinaryTree<Integer> bt = new BinaryTree<>();
long start = System.currentTimeMillis();
for (int i = 0; i < n; i++) {
bt.insert(i);
}
long btInsertTime = System.currentTimeMillis() - start;
start = System.currentTimeMillis();
for (int i = 0; i < n; i++) {
bt.search(i);
}
long btSearchTime = System.currentTimeMillis() - start;
// Test Binary Search Tree
BinarySearchTree<Integer> bst = new BinarySearchTree<>();
start = System.currentTimeMillis();
for (int i = 0; i < n; i++) {
bst.insert(i);
}
long bstInsertTime = System.currentTimeMillis() - start;
start = System.currentTimeMillis();
for (int i = 0; i < n; i++) {
bst.search(i);
}
long bstSearchTime = System.currentTimeMillis() - start;
System.out.println("Performance Comparison (n=" + n + "):");
System.out.println("Binary Tree:");
System.out.println(" Insertion: " + btInsertTime + "ms");
System.out.println(" Search: " + btSearchTime + "ms");
System.out.println("Binary Search Tree:");
System.out.println(" Insertion: " + bstInsertTime + "ms");
System.out.println(" Search: " + bstSearchTime + "ms");
}
}
Summary
| Aspect | Binary Tree | Binary Search Tree |
|---|---|---|
| Ordering | No constraints | Left < Root < Right |
| Search | O(n) - must check all nodes | O(log n) - use ordering |
| Insertion | O(n) - simple placement | O(log n) - maintain order |
| Applications | Expression trees, file systems | Database indexes, dictionaries |
| Complexity | Simple to implement | More complex but efficient |
| Memory | Same space usage | Same space usage |
| Balance | No guarantee | May become unbalanced |
Key Takeaways
- Binary Trees are simpler but less efficient for search operations
- Binary Search Trees provide fast search but require maintaining order
- Choose based on your primary use case: hierarchy vs search efficiency
- Both structures have the same space complexity
- BST operations are more complex but provide better performance
The choice between Binary Tree and Binary Search Tree depends on whether you need fast search operations and sorted data, or if you just need a hierarchical structure without ordering constraints.