Graph

Overview

This document provides a detailed comparison between different graph representations in Java, including Adjacency Matrix and Adjacency List. It covers their structures, operations, performance characteristics, visualizations, and practical applications. We’ll also explore a LeetCode example (Clone Graph) that combines graph and hash map usage.

Basic Definitions

What is a Graph?

A graph is a data structure consisting of a set of vertices (nodes) and a set of edges connecting pairs of vertices. Graphs can be:

  • Directed (edges have direction)
  • Undirected (edges have no direction)
  • Weighted (edges have weights)
  • Unweighted (edges have no weights)

Types of Graphs

  • Undirected Unweighted Graph: Social networks, friend relationships
  • Directed Weighted Graph: Road networks, flight routes

Visual Representation

Below is a simple undirected graph with 4 nodes and 5 edges:

   0
  / \
 1---2
  \ /
   3

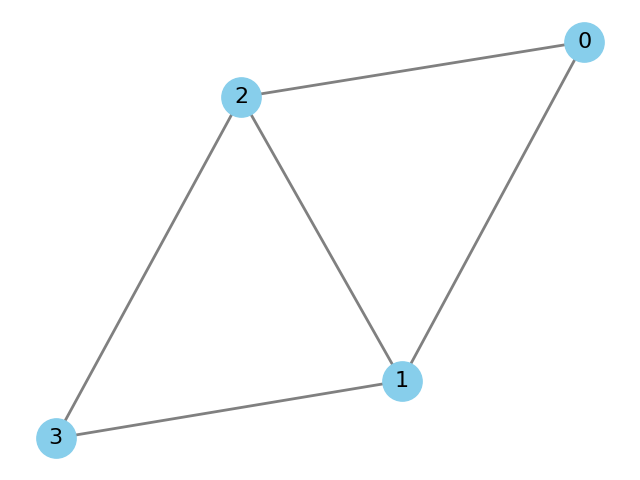Simple Undirected Graph Figure: A simple undirected graph with 4 nodes and 5 edges.

In the following sections, we will use this graph as an example to illustrate both the adjacency matrix and adjacency list representations.

Adjacency Matrix Representation 

  0 1 2 3
0 0 1 1 0
1 1 0 1 1
2 1 1 0 1
3 0 1 1 0

Figure: Adjacency matrix representation of the above graph.

The adjacency matrix is a 2D array where the entry at row i and column j is 1 if there is an edge between node i and node j, and 0 otherwise. This representation is simple and allows for fast edge lookups (O(1)), but it uses O(V²) space, making it inefficient for large, sparse graphs. It is best suited for dense graphs where most pairs of nodes are connected.

Adjacency List Representation 

0: 1, 2
1: 0, 2, 3
2: 0, 1, 3
3: 1, 2

Figure: Adjacency list representation of the above graph.

The adjacency list uses an array (or list) of lists, where each index represents a node and stores a list of its neighbors. This approach is memory-efficient for sparse graphs (O(V+E) space) and is the most common representation in practice. However, checking if an edge exists between two nodes may take O(degree) time, where degree is the number of neighbors of a node.

Mathematical Perspective: Laplacian Matrix and Eigenvalues

For a graph with adjacency matrix \(A\) and degree matrix \(D\) (where \(D_{ii}\) is the degree of node \(i\)), the Laplacian matrix \(L\) is defined as:

\[L = D - A\]

The eigenvalues of \(L\) are real and non-negative. The second smallest eigenvalue, usually denoted as \(\lambda_2\), is called the algebraic connectivity of the graph.

  • \(\lambda_2 > 0\) if and only if the graph is connected.
  • The larger \(\lambda_2\), the more robustly connected the graph is.
  • \(\lambda_2\) is widely used in spectral graph theory, network robustness, and consensus algorithms.

Example: For the above graph, you can compute $L$ and its eigenvalues to analyze its connectivity properties.

Visualizing $\lambda_2$ in Different Graphs

Below is a comparison of three graphs with different connectivity properties. The value of \(\lambda_2\) is shown in each subfigure title:

Comparison of lambda_2 in different graphs Figure: Left: Disconnected graph (\(\lambda_2 = 0\)). Middle: Connected but sparse graph (small \(\lambda_2\)). Right: Connected and dense graph (large \(\lambda_2\)).

  • Left: The graph is disconnected, so \(\lambda_2 = 0\).
  • Middle: The graph is globally connected but has few edges, so $\lambda_2$ is positive but small, indicating weak connectivity.
  • Right: The graph is globally connected and has many edges, so $\lambda_2$ is much larger, indicating strong connectivity and robustness.

This demonstrates how $\lambda_2$ quantitatively reflects the overall connectivity of a graph.

Structural Comparison

Aspect Adjacency Matrix Adjacency List
Space Complexity O(V^2) O(V + E)
Edge Lookup O(1) O(degree)
Add Edge O(1) O(1)
Remove Edge O(1) O(degree)
Iterate Neighbors O(V) O(degree)
Best For Dense graphs Sparse graphs
  • V: number of vertices
  • E: number of edges

Implementation in Java

Adjacency Matrix (Undirected Graph) 

class GraphMatrix {
    private int V;
    private int[][] matrix;

    public GraphMatrix(int V) {
        this.V = V;
        matrix = new int[V][V];
    }

    public void addEdge(int u, int v) {
        matrix[u][v] = 1;
        matrix[v][u] = 1; // undirected
    }

    public void removeEdge(int u, int v) {
        matrix[u][v] = 0;
        matrix[v][u] = 0;
    }

    public boolean hasEdge(int u, int v) {
        return matrix[u][v] == 1;
    }

    public void printMatrix() {
        for (int i = 0; i < V; i++) {
            for (int j = 0; j < V; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }
}

Adjacency List (Undirected Graph) 

import java.util.*;

class GraphList {
    private int V;
    private List<List<Integer>> adj;

    public GraphList(int V) {
        this.V = V;
        adj = new ArrayList<>();
        for (int i = 0; i < V; i++) {
            adj.add(new ArrayList<>());
        }
    }

    public void addEdge(int u, int v) {
        adj.get(u).add(v);
        adj.get(v).add(u); // undirected
    }

    public void removeEdge(int u, int v) {
        adj.get(u).remove((Integer)v);
        adj.get(v).remove((Integer)u);
    }

    public boolean hasEdge(int u, int v) {
        return adj.get(u).contains(v);
    }

    public void printList() {
        for (int i = 0; i < V; i++) {
            System.out.print(i + ": ");
            for (int vtx : adj.get(i)) {
                System.out.print(vtx + " ");
            }
            System.out.println();
        }
    }
}

Common Operations

Add Node / Edge

  • Adjacency Matrix: Add row/column (resize array), set matrix[u][v] = 1
  • Adjacency List: Add new list, add to neighbor lists

Remove Node / Edge

  • Adjacency Matrix: Set matrix[u][v] = 0
  • Adjacency List: Remove from neighbor lists

Search / Traversal

  • BFS (Breadth-First Search)
  • DFS (Depth-First Search)

BFS Example (Adjacency List) 

public void bfs(int start) {
    boolean[] visited = new boolean[V];
    Queue<Integer> queue = new LinkedList<>();
    visited[start] = true;
    queue.offer(start);
    while (!queue.isEmpty()) {
        int u = queue.poll();
        System.out.print(u + " ");
        for (int v : adj.get(u)) {
            if (!visited[v]) {
                visited[v] = true;
                queue.offer(v);
            }
        }
    }
}

DFS Example (Adjacency List) 

public void dfs(int u, boolean[] visited) {
    visited[u] = true;
    System.out.print(u + " ");
    for (int v : adj.get(u)) {
        if (!visited[v]) {
            dfs(v, visited);
        }
    }
}

Performance Analysis

Operation Adjacency Matrix Adjacency List
Add Edge O(1) O(1)
Remove Edge O(1) O(degree)
Check Edge O(1) O(degree)
Enumerate Neigh. O(V) O(degree)
Space O(V^2) O(V+E)
  • Adjacency Matrix is better for dense graphs (many edges)
  • Adjacency List is better for sparse graphs (few edges)

Applications

  • Social Networks: Users and friendships (undirected, sparse)
  • Maps/Navigation: Cities and roads (directed, weighted)
  • Web Links: Pages and hyperlinks (directed)
  • Scheduling: Tasks and dependencies (DAG)
  • Network Routing: Routers and connections

LeetCode Example: 133. Clone Graph (with HashMap)

Problem

Given a reference of a node in a connected undirected graph, return a deep copy (clone) of the graph. Use a hash map to avoid revisiting nodes.

LeetCode 133. Clone Graph

Java Solution (DFS + HashMap) 

class Node {
    public int val;
    public List<Node> neighbors;
    public Node() {
        val = 0;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val) {
        val = _val;
        neighbors = new ArrayList<Node>();
    }
    public Node(int _val, ArrayList<Node> _neighbors) {
        val = _val;
        neighbors = _neighbors;
    }
}

class Solution {
    private Map<Node, Node> visited = new HashMap<>();

    public Node cloneGraph(Node node) {
        if (node == null) return null;
        if (visited.containsKey(node)) {
            return visited.get(node);
        }
        Node clone = new Node(node.val);
        visited.put(node, clone);
        for (Node neighbor : node.neighbors) {
            clone.neighbors.add(cloneGraph(neighbor));
        }
        return clone;
    }
}

Explanation:

  • Use a HashMap<Node, Node> to map original nodes to their clones.
  • Prevents infinite loops and duplicate nodes.
  • Works for any connected undirected graph.

More LeetCode Graph Problems

    1. Course Schedule (Topological Sort)
    1. Number of Islands (DFS/BFS)
    1. Is Graph Bipartite?

Summary Table

Representation Space Edge Lookup Add Edge Remove Edge Iterate Neighbors Best For
Adjacency Matrix O(V^2) O(1) O(1) O(1) O(V) Dense Graphs
Adjacency List O(V + E) O(degree) O(1) O(degree) O(degree) Sparse Graphs
Edge List O(E) O(E) O(1) O(E) O(E) Simple Graphs

Key Takeaways

  1. Adjacency Matrix is simple and fast for dense graphs, but wastes space for sparse graphs.
  2. Adjacency List is memory-efficient for sparse graphs and is the most common representation.
  3. Edge List is useful for algorithms that process all edges (e.g., Kruskal’s MST).
  4. HashMap is often used in graph algorithms to track visited nodes or mappings (see LeetCode 133).
  5. Choose the representation based on the graph’s density and the operations you need to optimize.