Control Barrier Function with Basic Example

Finished

Here Let’s consider a simple example to illustrate the concept of Control Barrier Function.

Sytem Dynamics

Consider a simple system dynamics as:

\begin{equation} \dot{\mathbf{x}} = \mathbf{u} \end{equation}

where \(x\in\mathbb{R}^2\) and \(u\in\mathbb{R}^2\) denotes the control input.

Safety Set

Then we define the safe set \(\mathcal{H}\) as:

\begin{equation} h(\mathbf{x}) = 5- || \mathbf{x} || \geq 0 \end{equation}

\[\mathcal{H} = \{ \mathbf{x}\in\mathbb{R}^2 | h(\mathbf{x}) \geq 0 \} \tag{3}\]

By defining the safety set, we can ensure that the robot is always at most 5 units away from the origin.

Control Barrier Function

Following the definition of Control Barrier Function (refer to Theorem Control Barrier Function), we can define such constraints as:

\begin{equation} \dot{h}(\mathbf{x}, \mathbf{u}) = \nabla h(\mathbf{x}) \cdot \mathbf{u} \geq -\kappa(h(\mathbf{x})) \end{equation}

where \(\kappa(h(\mathbf{x}))\) is an extended class-\(\mathcal{K}\) function.

Example

First lets use a move-to-goal controller as:

\begin{equation} \mathbf{u}^\mathrm{ref} = -k(\mathbf{x} - \mathbf{x}^\mathrm{goal}) \end{equation}

Then to ensure the system state is safe , we can use the following Quadratic Program (QP) to solve for the control input:

\[\mathbf{u}^{*} = \arg\min_{\mathbf{u}} \frac{1}{2}||\mathbf{u} - \mathbf{u}^\mathrm{ref}||^2 \quad \\ \text{s.t.} \quad \nabla h(\mathbf{x}) \cdot \mathbf{u} \geq -\kappa(h(\mathbf{x}))\]

This can be solved using any QP solver. Here is the results:

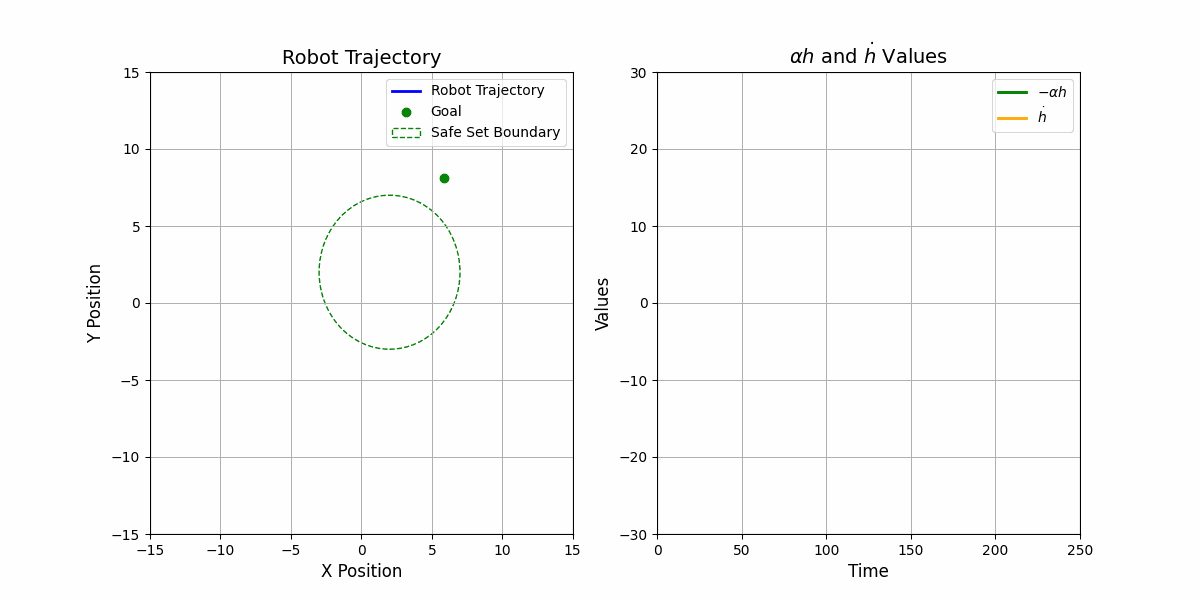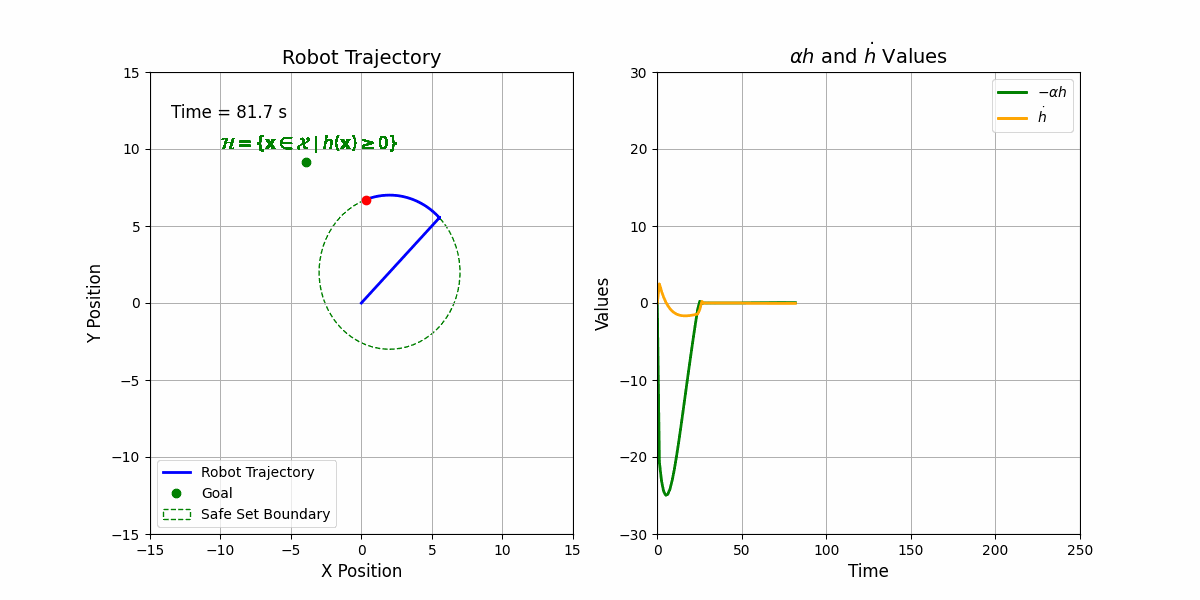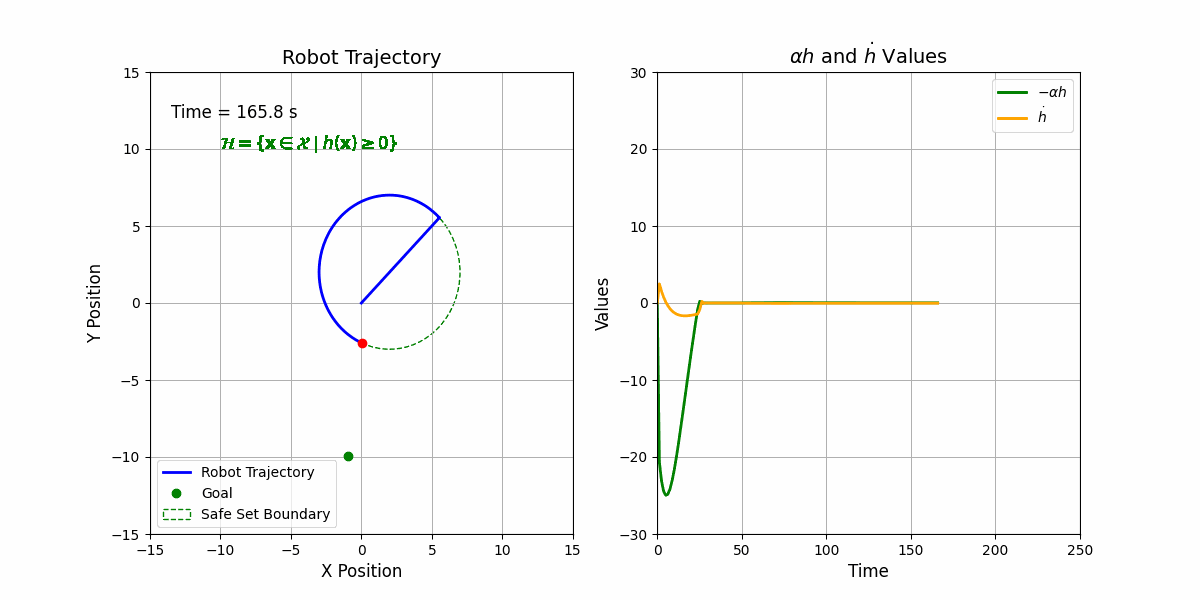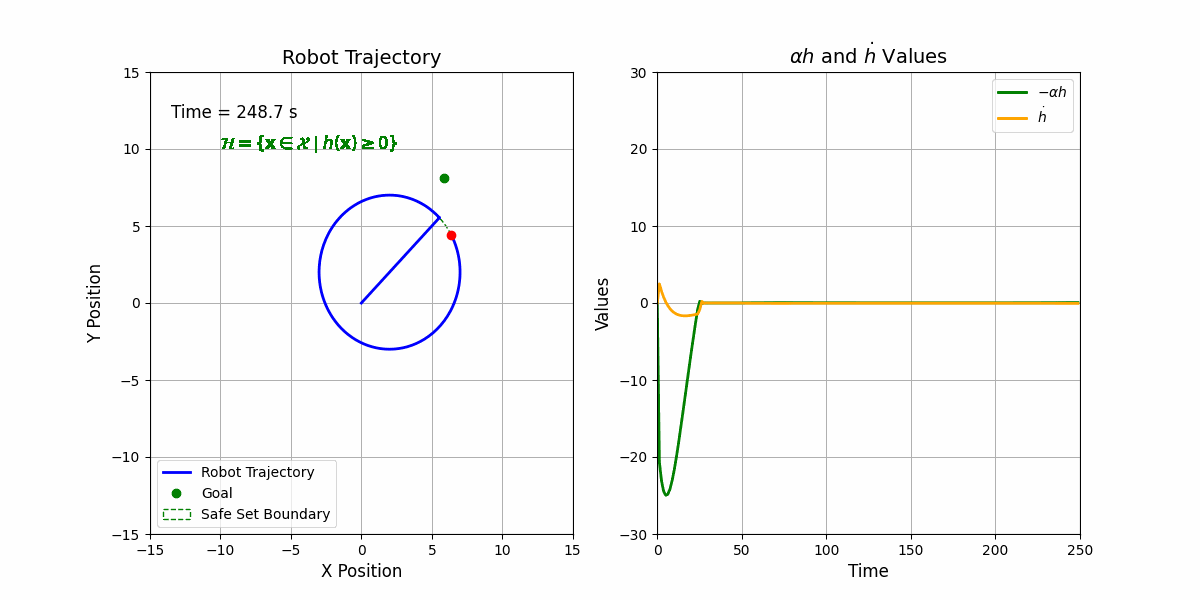
This is cool Right? It is very easy to develop with theorectical guarantee.